矢量搜索探索

Metadata

original_title: An exploration of vector search | Shalvah’s Blog

source: https://blog.shalvah.me/posts/an-exploration-of-vector-search

Notes

Summary

摘要： 本文探讨了向量搜索的基本理论和应用，提出了将数据库中的项目和输入项表示为向量的想法，以便找到与输入最接近的向量。作者首先介绍了向量的概念，指出向量不仅有大小（或长度），还有方向。在向量搜索中，大小并不是唯一重要的因素，而是更关注向量之间的相似性。接着，文章详细描述了四种常用的相似性计算方法：欧几里得距离、余弦相似度、曼哈顿距离和点积。这些方法各有适用场景，尤其在处理高维数据时，曼哈顿距离可能更为有效。作者通过一个车辆数据集的实例，展示了如何使用这些相似性度量来进行向量搜索，最后构建了一个简单的向量搜索引擎，并探讨了如何利用变换器生成向量。整体上，文章揭示了向量搜索在推荐系统等领域的潜力和应用。

要点总结：

1. 向量搜索的基本理念：向量搜索通过将数据库中的项和查询项表示为向量，寻找与输入项最接近的向量，以实现高效匹配和检索。
2. 向量的特性：向量不仅包含大小信息，还包含方向。在向量搜索中，方向更为重要，因为相同大小的向量可能具有不同的含义。
3. 相似性度量方法：文章介绍了四种相似性度量方法，分别是欧几里得距离、余弦相似度、曼哈顿距离和点积，适用于不同的应用场景，尤其是在高维数据处理时。
4. 实例应用：通过车辆数据集的例子，展示了如何使用这些相似性度量来进行向量搜索，并实现了一个简单的向量搜索引擎。
5. 向量生成：文章探讨了如何通过变换器生成向量，进一步扩展了向量搜索的应用潜力，尤其在推荐系统等领域的应用。

---

Origin

With the AI hype going around, you may have come across the phrase “vector search”, “vector database”, or “embeddings” lately. Here’s an exploration of what that means. I’m not a data scientist, but I was intrigued and decided to dig in.

最近，随着人工智能热潮的兴起，你可能会接触到 “矢量搜索”、“矢量数据库 “或 “嵌入 “等词语。下面我们就来探讨一下它们的含义。我不是数据科学家，但我很感兴趣，决定深入研究一下。

Basic Theory 基本理论

The idea behind vector search is: “What if we could represent the items in our database, as well as the input term, as vectors? We could then find the vectors which are closest to the input.” Let’s dig into that.

向量搜索背后的理念是”如果我们能用向量来表示数据库中的项目和输入词，会怎么样呢？然后，我们就能找到最接近输入项的向量”。让我们深入探讨一下。

Vectors 向量

Think of a vector as describing a movement from one point in space to another point. For instance, in the graph below, we can see some vectors in 2D space: is a vector from (100, 50) to (-50, -50), and is a vector from (0, 0) to (100, -50).

矢量描述的是从空间中的一点到另一点的运动。例如，在下图中，我们可以看到二维空间中的一些向量： 是一个从（100，50）到（-50，-50）的向量，而 是一个从（0，0）到（100，-50）的向量。

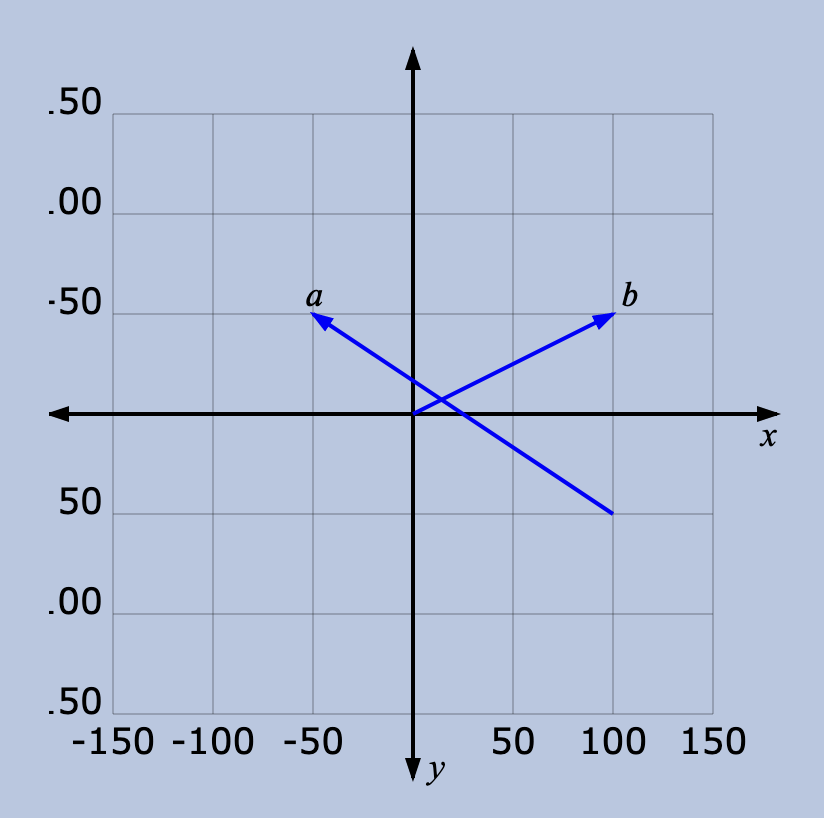
A lot of the time (and in the rest of this article), we deal with vectors starting from the origin (0, 0), such as . We can then omit the “from” part, and simply say is the vector (100, -50).

很多时候（以及在本文的其余部分），我们处理的向量都是从原点（0，0）开始的，例如 。我们可以省略 “从 “的部分，简单地说 是向量（100，-50）。

How do we extend the idea of vectors to non-numerical entities?

如何将向量的概念扩展到非数字实体呢？

Dimensions 维数

As we’ve seen, each numerical vector has x and y coordinates (or x, y, z in a 3D system, and so on). x, y, z… are the axes, or dimensions of this vector space. Given some non-numerical entities we want to represent as vectors, we need to first decide on the dimensions, and assign a value to each entity for each dimension.

正如我们所见，每个数字向量都有 x 和 y 坐标（或三维系统中的 x、y、z，等等）。如果我们想要用向量来表示一些非数值实体，我们首先需要确定维数，并为每个实体的每个维数赋值。

For example, in a dataset of vehicles, we could define four dimensions: “number of wheels”, “moves on land”, “has an engine”, and “max occupants”. Then we could represent some vehicles as:

例如，在一个车辆数据集中，我们可以定义四个维度：“车轮数量”、“在陆地上行驶”、“有发动机 “和 “最多乘员”。然后，我们可以将一些车辆表示为

item 项目	number of wheels 车轮数量	has an engine 有发动机	moves on land 在陆地上行驶	max occupants 最多乘员
car 汽车	4	yes 是	yes 是	5
bicycle 自行车	2	no 无	yes 是	1
tricycle 三轮车	3	no 无	yes 是	1
motorcycle 摩托车	2	yes 是	yes 是	2
sailboat 帆船	0	no 无	no 无	20
ship 船	0	yes 是	no 无	1000

So, our car vector would be (4, yes, yes, 5), or numerically, (4, 1, 1, 5) (putting yes = 1, no = 0).

因此，我们的汽车向量将是（4、是、是、5），或者用数字表示为（4、1、1、5）（是=1，否=0）。

Dimensions are a way for us to (try to) capture the semantic meaning of an entity and represent it by numbers. For this reason, they are subjective. There’s no requirement to pick these specific dimensions. We could instead use, “has wings”, “uses diesel”, “top speed”, “average weight”, “price”, or whatever.

维度是我们（试图）捕捉实体语义并用数字表示的一种方式。因此，它们是主观的。我们并不需要选择这些特定的维度。我们可以使用 “有机翼”、“使用柴油”、“最高车速”、“平均重量”、“价格 “或其他任何词语。

Dimensions are also called features or facets. They are an extremely important part of vector search (and data science/machine learning in general). We’ll see soon how the number and choice of dimensions can affect the search. For now, let’s continue with the next foundation of vector search.

维度也称为特征或面。它们是向量搜索（以及一般数据科学/机器学习）中极其重要的一部分。我们很快就会看到维度的数量和选择会如何影响搜索。现在，让我们继续了解向量搜索的下一个基础。

Similarity 相似性

With vector search, we want to return items by closeness to the search term. For example, if a user searches for “car”, you want to be able to return results which mention “automobile” and “vehicle” as well. Vector search is one way to address that.

在向量搜索中，我们希望通过与搜索词的相似度来返回项目。例如，如果用户搜索 “汽车”，你希望返回的结果中也能提到 “汽车 “和 “车辆”。矢量搜索就是解决这个问题的一种方法。

Vector searches are also used in recommender systems. For example, recommending similar products, articles, shows, or songs to a customer based on something they already liked. In this case, the input is already part of the dataset.

矢量搜索也可用于推荐系统。例如，根据客户已经喜欢的东西向他们推荐类似的产品、文章、节目或歌曲。在这种情况下，输入已经是数据集的一部分。

So the question is how do we determine which are most similar?

那么问题来了，我们如何确定哪些最相似呢？

We have to start by defining what we mean by similar. Every vector has a magnitude (aka length, or size) and direction. For instance, in this graph, and are pointing in the same direction, but are of different lengths. and are in exactly opposite directions, but have the same magnitude. And then there’s , a bit shorter than , and not pointing in the exact direction, but close.

我们必须先定义相似的含义。每个矢量都有大小（又称长度或尺寸）和方向。例如，在这幅图中， 和 指向同一个方向，但长度不同。 和 方向完全相反，但幅度相同。还有 ，比 短一点，指向的方向不完全相同，但也很接近。

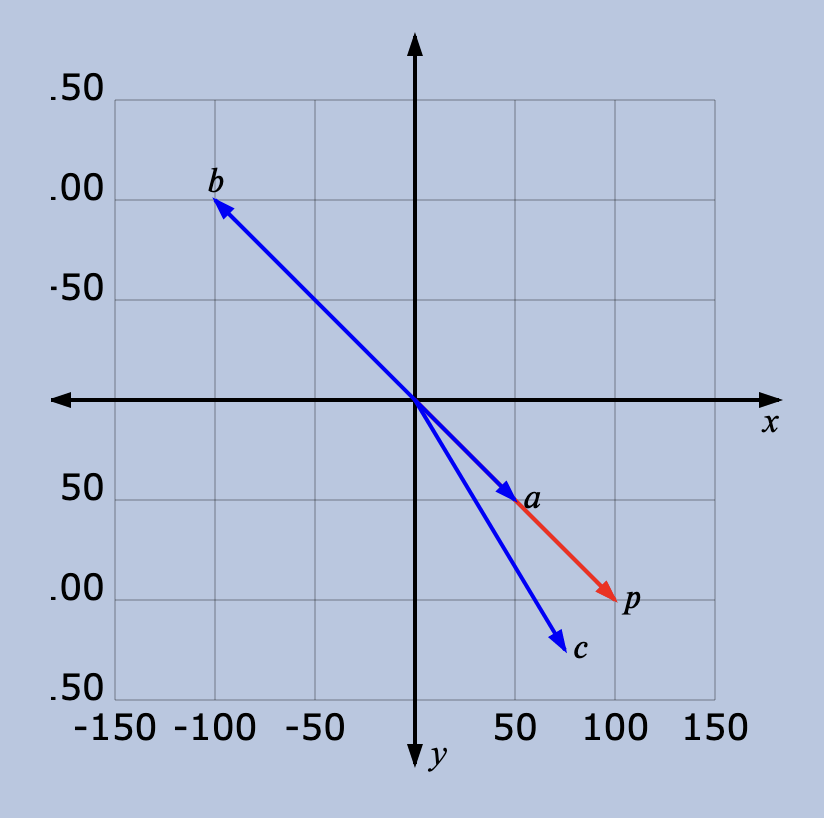
So which is most similar to ?

那么，哪个与 最相似呢？

• If “similar” means pointing in a similar direction only, then is the most similar to . Next up is . is the least similar, since it points exactly opposite to p

  如果 “相似 “仅指指向相似的方向，那么 与 最相似。接下来是 。 是最不相似的，因为它的指向正好与 p 相反。

• If “similar” means similar magnitude only, then is the most similar to (since it has the same length) followed by , and then .

  如果 “相似 “仅指大小相似，那么 与 最相似（因为它具有相同的长度），其次是 ，然后是 。

In vector search, we rarely look at size alone. This is because you can easily get a vector with totally different values in each dimension but the same overall length (for instance, b is the same length as p, but points exactly opposite). Since vectors are often used to describe semantic meaning, looking at length alone will rarely give you what you want. Most measures of similarity either depend only on the direction, or both the direction and size.

在向量搜索中，我们很少只看大小。这是因为你很容易得到一个在每个维度上都有完全不同的值，但总长度相同的向量（例如，b 和 p 的长度相同，但点数正好相反）。由于向量通常用于描述语义，因此只看长度很少能得到想要的结果。大多数相似性度量要么只取决于方向，要么同时取决于方向和大小。

Measures of similarity 相似性度量

Here are four ways vector similarity is often calculated:

以下是通常计算向量相似性的四种方法：

• Euclidean distance: The direct distance between the “tips” of the two vectors. The Euclidean distance is 0 when the two vectors are the same, and increases as the angle (direction) or magnitude (length) of either increases. So, for a vector, p, we can compute the distances to all other vectors and pick the one with the smallest.

  欧氏距离：两个向量 “顶端 “之间的直接距离。当两个向量相同时，欧氏距离为 0，随着角度（方向）或大小（长度）的增加，欧氏距离也会增加。因此，对于一个向量 p，我们可以计算它与所有其他向量的距离，然后选出最小的一个。

• Manhattan distance: This is also the distance between the “tips”, but assuming you were only allowed to walk parallel to the axes (left, right, up, down).

  曼哈顿距离：这也是 “尖 “与 “尖 “之间的距离，但假定你只能平行于轴线（左、右、上、下）行走。

• Dot product: You get this by multiplying the corresponding dimensions from the vectors, and adding them up (ie ). This is a useful formula since it uses the dimensions of the two vectors, which means it accounts for both direction and magnitude.

  点积：将两个向量的相应维数相乘，然后相加（即 ）即可得到。这是一个有用的公式，因为它使用了两个矢量的维数，这意味着它同时考虑了方向和大小。

• Cosine similarity: This works by finding the cosine of the angle between the two vectors (which means cosine similarity doesn’t consider magnitude, just direction). We get this by dividing the dot product by the product of the two lengths, ie .

  余弦相似度：其原理是求出两个矢量之间夹角的余弦（这意味着余弦相似性不考虑大小，只考虑方向）。我们用点积除以两个长度的乘积，即 ，就得到了余弦相似度。

This graph shows the four measures for to another vector . Drag the tips of the vectors to reposition them, and watch how the values change. (Some things to try: putting the vectors at right angles to each other, putting them directly opposite each other, giving them the same magnitudes).

该图显示了 与另一个向量 的四种测量方法。拖动矢量的顶端来调整它们的位置，观察它们的值是如何变化的。(可以尝试的方法有：将矢量成直角，将它们放在正对面，使它们的大小相同）。

Euclidean distance, in green: 55.900000000000006

欧氏距离，绿色：55.900000000000006

Manhattan distance, in blue: 75

曼哈顿距离, 蓝色:75

Dot product (): 17500

点积 ( ):17500

cosθ: 0.919

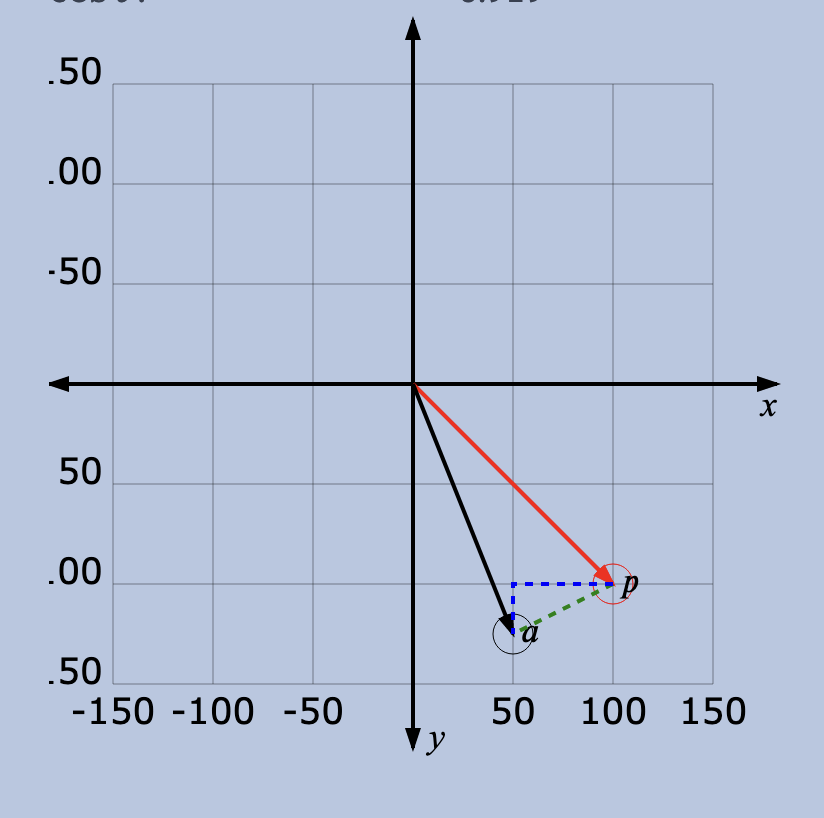
From this, we can see some useful facts about these measures, and how to choose:

由此，我们可以看到有关这些措施的一些有用事实，以及如何选择：

The Euclidean distance is 0 if the vectors are exactly the same. As the size of one vector or the angle between them changes, it increases indefinitely. This is probably the most straightforward measure (smaller = more similar), and it’s quite commonly used. The Manhattan distance behaves similarly (0 when equal, then increases).

如果向量完全相同，欧氏距离为 0。当一个向量的大小或它们之间的角度发生变化时，它就会无限增大。这可能是最直接的测量方法（越小 = 越相似），也是最常用的方法。曼哈顿距离也有类似的表现（相等时为 0，然后增加）。

The dot product starts at some number (not 0) when the two vectors are equal. If you keep the sizes of the two equal, and increase the angle, the dot product decreases, reaching 0 when the two vectors are at right angles. Keep on increasing the angle, and it decreases until they are directly opposite each other, then increases again until you get back to the start. On the other hand, if you increase the size of while keeping the angle constant, the dot product just keeps increasing.

当两个向量相等时，点积从某个数（而不是 0）开始。如果保持两个矢量的大小相等，并增大角度，点积就会减小，当两个矢量成直角时，点积为 0。继续增大角度，点积就会减小，直到两个矢量直接相对，然后再增大，直到回到起点。另一方面，如果在保持角度不变的情况下增大 的大小，点积就会不断增大。

This non-uniform distribution makes the dot product trickier to use (there is no maximum value; a smaller dot product could mean less similar or more similar). It’s also non-unique; there are multiple different positions for that will give you the same dot product as when = . The dot product typically only makes sense when we can normalize all vectors to have the same length (at which point, it becomes equal to the cosine similarity).

这种非均匀分布使得点积的使用更加棘手（没有最大值；点积越小可能意味着相似度越低，也可能意味着相似度越高）。它也不是唯一的； 有多个不同的位置，可以得到与 = 相同的点积。通常，只有当我们可以将所有向量归一化为具有相同长度时，点积才有意义（此时，点积等于余弦相似度）。

Cosine similarity simply looks at the angle between the two vectors (or more accurately, the cosine of the angle). This means that the result is always between 1 and -1, while the dot product can be any number. The cosine is 1 when the vectors are exactly the same; it decreases to 0 when they’re at right angles, and then -1 when they’re exactly opposite. Such a neat property. Its disadvantage is that it does not consider the magnitudes—the cosine will have the same value for all vectors pointing in a certain direction, regardless of their length. Hence cosine similarity is often only used when all vectors in the dataset are of the same length, or we don’t care about their lengths.

余弦相似度只需查看两个矢量之间的角度（或更准确地说，角度的余弦）。这意味着结果总是介于 1 和 -1 之间，而点积可以是任何数字。当两个矢量完全相同时，余弦值为 1；当两个矢量成直角时，余弦值减小为 0；当两个矢量完全相反时，余弦值减小为-1。这是一个非常巧妙的性质。它的缺点是不考虑大小—所有指向某个方向的矢量，无论其长度如何，余弦值都是相同的。因此，余弦相似度通常只在数据集中的所有向量长度相同，或者我们不关心它们的长度时使用。

A second disadvantage of the cosine is that it’s more computationally expensive. To find the dot product, you need to multiply the dimensions for each vector together and add them up. To find the cosine similarity, you have to divide the dot product by the product of the two vectors’ magnitudes. This doesn’t seem like a big deal, but in a large database, with thousands or millions of vectors, each having hundreds or thousands of dimensions, this takes valuable CPU time. This is why Elasticsearch recommends using the dot product with all vectors normalized to the same length.

余弦值的第二个缺点是计算成本较高。要计算点积，需要将每个向量的维数相乘，然后相加。而要求得余弦相似度，则需要用点积除以两个向量的大小之积。这看起来没什么大不了的，但在大型数据库中，有数千或数百万个向量，每个向量都有数百或数千个维度，这就需要耗费宝贵的 CPU 时间。因此，Elasticsearch 建议使用点积，并将所有向量归一化为相同长度。

So how do you choose which measure to use? In practice, it boils down to knowing your data, and experimenting to see what gives you the best results. I’m no data scientist, but here’s what I gleaned from the Internet:

那么，如何选择使用哪种测量方法呢？实际上，这可以归结为了解你的数据，并通过实验来了解什么能给你带来最好的结果。我不是数据科学家，但以下是我从互联网上搜集到的信息：

• The Euclidean distance is a “safe” default to use when you don’t know much about your data.

  在对数据不甚了解的情况下，欧氏距离是一种 “安全 “的默认值。

• If all vectors have the same length (or can be normalized to do so), cosine similarity/dot product is probably a good choice.

  如果所有向量的长度相同（或可以归一化），余弦相似度/点乘可能是一个不错的选择。

• The Manhattan distance might be a better measure if the vectors have a high number of dimensions (research paper [PDF], StackExchange).

  如果向量的维数较高，曼哈顿距离可能是更好的测量方法（研究论文 [PDF]，StackExchange）。

A basic example 一个基本例子

Let’s plot our dataset of vehicles. Since my graph can only represent two dimensions, I’ll take two dimensions from the table—“number of wheels” and “has an engine”. Let’s plot our vectors. Note that “number of wheels” is a continuous dimension (values from 0 and up), while “has an engine” is yes or no (0/1). This gives us the following vectors:

让我们绘制车辆数据集。由于我的图表只能表示两个维度，因此我将从表格中提取两个维度—“车轮数量 “和 “有发动机”。让我们绘制矢量图。请注意，“车轮数量 “是一个连续维度（数值从 0 到 0），而 “是否有发动机 “则是 “是 “或 “否”（0/1）。这样我们就得到了以下向量：

car: (4, yes)  汽车：（4，是）

bicycle: (2, no)

自行车：（2，否）

tricycle: (3, no)

三轮车：（3，否）

motorcycle: (2, yes)

摩托车：（2，有）

sailboat: (0, no)

帆船：（0，否）

ship: (0, yes)  轮船：（0，有）

Also, imagine we’re searching for a vehicle which has three wheels and also has an engine. That is the vector (3, yes), represented by P on the graph below. You can see that there’s no such vehicle in our set, but the “most similar” within our current dimensions is the tricycle according to the Euclidean and Manhattan distances, but the car according to the cosine. You can try dragging the vector P around, and watch how the closest changes. Sometimes all three measures choose different vectors!

另外，假设我们要搜索的是一辆有三个轮子并且有发动机的汽车。这就是向量 (3，是)，在下图中用 P 表示。您可以看到，在我们的集合中并没有这样的车辆，但是根据欧几里得距离和曼哈顿距离，在我们当前的维度内 “最相似 “的是三轮车，而根据余弦距离，最相似的是汽车。你可以试着拖动向量 P，看看最接近的向量是如何变化的。有时这三种测量方法会选择不同的向量！

Closest by Euclidean distance, in green: Tricycle (0.5)

按欧氏距离计算的最近距离，绿色：Tricycle (0.5)

Closest by Manhattan distance, in blue: Tricycle (0.5)

按曼哈顿距离计算最接近，蓝色：Tricycle (0.5)

Closest by normalized dot product/cosine: Car (0.997)

按归一化点积/余弦值计算最接近：汽车 (0.997)

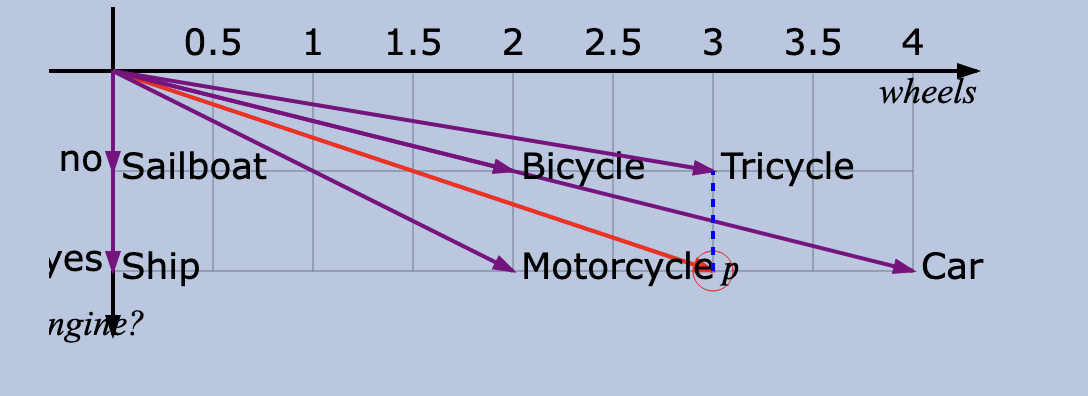
Voila, we have a very basic visual demo of vector search! Let’s write this as code.

瞧，我们有了一个非常基本的向量搜索可视化演示！让我们把它写成代码。

PS: You’ll notice that no/yes on this graph maps to 0.5/1, rather than 0/1. This is partly for visualization reasons (to make it easier to see on the graph), and partly for technical reasons (the cosine calculation tries to divide by the vector’s magnitude, which is impossible if the vector is 0). This is why you generally avoid having zero vectors in your dataset.

PS：你会注意到，这个图上的 “否”/“是 “映射为 0.5/1，而不是 0/1。这一方面是出于可视化的考虑（使图形更容易看清），另一方面也是出于技术原因（余弦计算试图除以矢量的大小，如果矢量为 0，这是不可能的）。这也是为什么通常要避免在数据集中出现零向量的原因。

Implementing 实施

Maths refresher: Here are the formulae we’re implementing to compute the similarity of two vectors and (click to expand)

数学复习：下面是我们要实现的计算两个向量 和 相似度的公式（点击展开）

Euclidean distance (): Pair the corresponding dimensions of each vector together, find their difference, and square it. Then add everything together and take the square root. For 2D vectors, this is , but in general, .

Manhattan distance (): Pair the corresponding dimensions of each vector together, find their difference, and take its absolute value (change negatives to positives). Then add everything together. For 2D vectors, this is , but in general, .

Dot product (): Pair the corresponding dimensions of each vector together and multiply them, then add everything together. For 2D vectors, this is , but in general, .

Cosine (): Find the magnitude of the two vectors, multiply them together, and divide the dot product by that. In maths notation, this is . For 2D vectors, the magnitude is .

Here’s a basic vector db in Ruby:

下面是 Ruby 中的基本向量 db：

class VectorDb
  attr_reader :vectors

  def initialize
    @vectors = {}
  end

  def add(**new_vectors)
    vectors.merge!(new_vectors)
  end

  def find_similar(vector, measure: :cosine, results: 3)
    vectors_with_distances =
      vectors.map do |other_vector_name, other_vector_dimensions|
        # The search vector may have some dimensions missing,
        # so we remove those from all vectors so that they don't factor into the search
        normalized_search_vector = search_vector.reject { |d| d.nil? }
        normalized_other_vector =
          other_vector_dimensions.reject.with_index { |b_i, i| search_vector[i].nil? }
        [other_vector_name, distance(normalized_search_vector, normalized_other_vector, measure)]
      end
      
    if measure == :cosine
      vectors_with_distances.max_by(results) { |name, distance| distance }.to_h
    else
      vectors_with_distances.min_by(results) { |name, distance| distance }.to_h
    end
  end

  private

  def distance(vector, other_vector, measure)
    __send__(measure, vector, other_vector)
  end

  def euclidean(vec_a, vec_b)
    Math.sqrt(
      vec_a.zip(vec_b).map { |(a_i, b_i)| (a_i - b_i) ** 2 }.sum
    )
  end

  def manhattan(vec_a, vec_b)
    vec_a.zip(vec_b).map { |(a_i, b_i)| (a_i - b_i).abs }.sum
  end

  def dot_product(vec_a, vec_b)
    vec_a.zip(vec_b).map { |(a_i, b_i)| a_i * b_i }.sum
  end

  def cosine(vec_a, vec_b)
    dot_product(vec_a, vec_b) / (magnitude(vec_a) * magnitude(vec_b))
  end

  def magnitude(vec)
    Math.sqrt(vec.map { |v_i| v_i ** 2 }.sum)
  end
end

Let’s test this vector database with the example of and above:

让我们以上面的 和 为例，测试一下这个向量数据库：

db = VectorDb.new
db.add(a: [50, 125])

p = [100, 100]
p db.find_similar(p, measure: :euclidean)
p db.find_similar(p, measure: :manhattan)
p db.find_similar(p, measure: :cosine)

This gives:  这就给出了

{:a => 55.90169943749474}
{:a => distance=>75}
{:a => distance=>0.9191450300180579}

This implementation is super basic. The vectors are stored as a simple list, and we search through all the vectors to compute the scores for the chosen measure. This would be unbearably slow in a real-world application.

这种实现方式非常简单。矢量存储为一个简单的列表，我们搜索所有矢量来计算所选测量的分数。这在实际应用中会非常慢。

Let’s bring our example dataset of vehicles to use with this vector database, still using the same two dimensions.

让我们将车辆示例数据集与矢量数据库一起使用，仍然使用相同的两个维度。

db = VectorDb.new
# Dimensions used are:
# - number of wheels: (0, ...)
# - has engine: (0.5, 1)
vehicles = {
  car: [4, 1],
  bicycle: [2, 0.5],
  tricycle: [3, 0.5],
  motorcycle: [2, 1],
  sailboat: [0, 0.5],
  ship: [0, 1],
}
db.add(**vehicles)

p = [3, 1]
puts "Euclidean (smaller is better):"
puts db.find_similar(p, measure: :euclidean)
puts "Manhattan (smaller is better):"
puts db.find_similar(p, measure: :manhattan)
puts "Cosine (bigger is better):"
puts db.find_similar(p, measure: :cosine)

Euclidean (smaller is better):
{:tricycle=>0.5, :motorcycle=>1.0, :car=>1.0}
Manhattan (smaller is better):
{:tricycle=>0.5, :motorcycle=>1, :car=>1}
Cosine (bigger is better):
{:bicycle=>0.9970544855015815, :car=>0.9970544855015815, :motorcycle=>0.9899494936611664}

This matches our results from the graph.

这与图表中的结果一致。

Choosing scales 选择刻度

In the earlier graph, I explained why we used 0.5/1 on our Boolean scale. But why not 1/2, 15/30, or some other scale? Well, we could, too. The graph would look slightly different, but how would our search results change? Let’s compute in code:

在前面的图表中，我解释了为什么我们使用 0.5/1 的布尔标度。但为什么不是 1/2、15/30 或其他比例呢？我们也可以这样做。图表看起来会略有不同，但我们的搜索结果会有什么变化呢？让我们用代码计算一下：

puts 'With 1/2:'
db = VectorDb.new
db.add(
  car: [4, 2],
  bicycle: [2, 1],
  tricycle: [3, 1],
  motorcycle: [2, 2],
  sailboat: [0, 1],
  ship: [0, 2],
)

p = [3, 2]
# ...

puts 'With 15/30:'
db = VectorDb.new
db.add(
  car: [4, 30],
  bicycle: [2, 15],
  tricycle: [3, 15],
  motorcycle: [2, 30],
  sailboat: [0, 15],
  ship: [0, 30],
)

p = [3, 30]
# ...

-----
With 1/2:
Euclidean:
{:tricycle=>1.0, :car=>1.0, :motorcycle=>1.0}
Manhattan:
{:tricycle=>1, :car=>1, :motorcycle=>1}
Cosine:
{:bicycle=>0.9922778767136677, :car=>0.9922778767136677, :motorcycle=>0.98058067569092}
-----
With 15/30:
Euclidean:
{:car=>1.0, :motorcycle=>1.0, :ship=>3.0}
Manhattan:
{:car=>1, :motorcycle=>1, :ship=>3}
Cosine:
{:bicycle=>0.9994594068217016, :car=>0.9994594068217016, :motorcycle=>0.9994522288395831}

This is very interesting. Even though the two Boolean values remain in a constant ratio, the search results change (although not significantly).

这一点非常有趣。尽管两个布尔值的比例保持不变，但搜索结果却发生了变化（尽管变化不大）。

With an “unbalanced” scale such as 15/100:

采用 “不平衡 “比例，如 15/100：

• We’ll get the same distance results (Euclidean and Manhattan) for other “yes” vectors (100s), since our input is also a yes

  对于其他 “是 “向量（100 个），我们将得到相同的距离结果（欧氏距离和曼哈顿距离），因为我们的输入也是 “是”。

• However, the distance from the “no” vectors will be affected. In our example, this doesn’t change much, but in a multi-dimensional search, it can have a bigger impact.

  但是，“否 “向量的距离会受到影响。在我们的示例中，这不会有太大变化，但在多维搜索中，影响可能会更大。

db.add(
  car: [4, 100],
  bicycle: [2, 15],
  tricycle: [3, 15],
  motorcycle: [2, 100],
  sailboat: [0, 15],
  ship: [0, 100],
)
p = [3, 100]

With 15/100:
Euclidean:
{:car=>1.0, :motorcycle=>1.0, :ship=>3.0}
Manhattan:
{:car=>1, :motorcycle=>1, :ship=>3}
Cosine:
{:car=>0.9999501235160887, :motorcycle=>0.9999500636867455, :sailboat=>0.9995503035223668}

This leads us to talk about the “weight” of a dimension. The reason the search results are affected is because all dimensions are being compared equally in the similarity calculations. For example, in the 15/30 example, there is a distance of 15 points between not having an engine and having one. This means that this is equivalent to a gap of 15 wheels. This makes the distance between yes and no larger than the distance between 2/3/4 wheels. So, given a search vector of “has engine” (= 30), our similarity scores will favour other vectors with an engine much more, even if they fall far of our other criteria.

这就引出了维度的 “权重 “问题。搜索结果之所以会受到影响，是因为在相似性计算中，所有维度的比较都是相同的。例如，在 15/30 的例子中，没有发动机和有发动机之间有 15 个点的距离。这意味着这相当于 15 个车轮的差距。这使得有和没有之间的距离大于 2/3/4 个车轮之间的距离。因此，给定一个 “有发动机”（= 30）的搜索向量，我们的相似性得分会更倾向于其他有发动机的向量，即使它们远远达不到我们的其他标准。

Conversely, the first version (0.5/1), has a distance of “0.5 wheels” between having an engine and not having one, so the engine part of the query has much less impact (as evidenced by the fact that tricycle ranks highest).

相反，在第一个版本（0.5/1）中，有发动机和没有发动机之间的距离为 “0.5 个轮子”，因此查询中发动机部分的影响要小得多（三轮车排名最高就证明了这一点）。

This demonstrates the importance of choosing a good scale. This applies not only to Boolean dimensions: a dimension such as “number of occupants” which can vary from 1 to thousands will affect our search results drastically.

这说明了选择一个好比例的重要性。这不仅适用于布尔维度：像 “乘员人数 “这样的维度，其变化范围可以从 1 到数千，这将对我们的搜索结果产生巨大影响。

Multi-dimensional vectors and embeddings

多维向量和嵌入

Since we aren’t constrained to the 2D graph anymore, we can move further and add all our dimensions.

由于我们不再受限于二维图形，我们可以更进一步，添加所有维度。

db = VectorDb.new

# Dimensions used are:
# - number of wheels: (0, ...)
# - has engine: (0.5, 1)
# - moves on land: (0.5, 1)
# - max occupants: (1, ...)
vehicles = {
  car: [4, 1, 1, 5],
  bicycle: [2, 0.5, 1, 1],
  tricycle: [3, 0.5, 1, 1],
  motorcycle: [2, 1, 1, 2],
  sailboat: [0, 0.5, 0.5, 20],
  ship: [0, 1, 0.5, 1000],
}
db.add(**vehicles)

Let’s search for a vehicle which moves on land and can carry 50 people. We don’t care about the number of wheels, but we want an engine,

让我们来寻找一辆能在陆地上行驶并能搭载 50 人的汽车。我们不在乎车轮的数量，但我们想要一个发动机、

p = [nil, 1, 1, 50]

Our search algorithm in find_similar accounts for this nil value by removing any missing dimensions from both search and dataset vectors, so they don’t affect the results.

我们在 find_similar 中的搜索算法会考虑到这个 nil 值，从搜索向量和数据集向量中删除任何缺失的维度，这样它们就不会影响搜索结果。

Euclidean:
{:sailboat=>30.008332176247315, :car=>45.0, :motorcycle=>48.0}
Manhattan:
{:sailboat=>31.0, :car=>45, :motorcycle=>48}
Cosine:
{:sailboat=>0.9999750508588203, :ship=>0.9996296030790003, :car=>0.9695607054902212}

All three measures rank sailboat highest, even though it has no engine and does not move on land. This is because of the weight of the “max occupants” dimension—its large values such as 20 and 1000 will dominate the simple 0.5/1 of the Booleans and 0-4 of the wheels. To make things more even, we can do two things:

尽管帆船没有发动机，也不在陆地上行驶，但所有三种测量方法都将帆船排在首位。这是因为 “最大乘员 “维度的权重—它的大数值，如 20 和 1000，将优先于布尔值的 0.5/1 和轮子值的 0-4。为了使事情更加公平，我们可以做两件事：

1. Change “moves on land” to spread out the values more (for instance, to 20 and 100 instead of 0.5 and 1)

   更改 “陆地上的移动”，使数值更加分散（例如，改为 20 和 100，而不是 0.5 和 1）

2. Change “occupants” to use buckets, rather than going from 0 to infinity. One such scale could be 1, 2, 3-6, 7-10, 10-15, 15-30, 30-60, 60-100.

   将 “居住者 “改为使用桶，而不是从 0 到无穷大。其中一个刻度可以是 1、2、3-6、7-10、10-15、15-30、30-60、60-100。

There’s no “right” result. There are a lot of subjective tuning decisions, which means two data scientists can have the same dataset and same general algorithms, but differing results. Choosing the right dimensions, choosing which dimensions to drop to avoid overfitting results, choosing dimensions could at query time, choosing how to represent dimensions, etc.

没有 “正确 “的结果。有很多主观的调整决定，这意味着两个数据科学家可以拥有相同的数据集和相同的通用算法，但结果却不同。选择正确的维度，选择放弃哪些维度以避免过度拟合结果，在查询时选择维度，选择如何表示维度，等等。

In the real world, we deal with more data like this—sentences, paragraphs, topics, products, images, etc. As you can see, this process of determining dimensions (feature engineering) can be quite difficult and time-consuming. Not only do you need to be intensely familiar with the data (gigabytes? terabytes? petabytes?) in order to recognize what dimensions are important, you also need to experiment to find the most suitable dimensions.

在现实世界中，我们会处理更多类似的数据—句子、段落、主题、产品、图片等。正如您所看到的，确定维度（特征工程）的过程可能相当困难和耗时。您不仅需要非常熟悉数据（千兆字节、兆兆字节、千万兆字节），以识别哪些维度是重要的，还需要进行试验，以找到最合适的维度。

Additionally, there’s the task of converting the input to a vector (except in recommender systems), which requires automated semantic analysis.

此外，还需要将输入转换成向量（推荐系统除外），这就需要进行自动语义分析。

There is an alternative. With vector embeddings, you can train a model (or use a pretrained model) which handles this, classifying the dataset to come up with several dimensions. For better results in specialised domains, you may still want to combine with some manual feature extraction.

有一种替代方法。使用向量嵌入，你可以训练一个模型（或使用预训练模型）来处理这个问题，对数据集进行分类，从而得出几个维度。为了在专业领域取得更好的效果，你可能还需要结合一些手动特征提取。

Let’s play with embeddings a bit. We’ll use this library, @xenova/transformers. Transformers are one technique for generating embeddings of text. Using a library rather than an API means that all analysis and classification is done locally, so the library must come with its own inbuilt corpus of words. (This library’s size is 46 MB!)

让我们来玩一下嵌入。我们将使用 @xenova/transformers 库。变换器是生成文本嵌入的一种技术。使用库而非 API 意味着所有的分析和分类都在本地完成，因此库必须自带内置词库。(该库的大小为 46 MB！）。

I couldn’t find any libraries for Ruby, so this means porting the vector database to JavaScript:

我找不到任何 Ruby 库，因此这意味着要将矢量数据库移植到 JavaScript：

class VectorDb {
  vectors = {};

  add(newVectors) {
    Object.assign(this.vectors, newVectors)
  }

  findSimilar(searchVector, measure, results = 3) {
    let vectorsWithDistances =
      Object.entries(this.vectors).map(([otherVectorName, otherVectorDimensions], _) => {
      let normalizedSearchVector = searchVector.filter(d => d !== null);
      let normalizedOtherVector =
        otherVectorDimensions.filter((b_i, i) => searchVector[i] !== null)
      return [otherVectorName, this.distance(normalizedSearchVector, normalizedOtherVector, measure)]
    }).sort((v1, v2) => v1[1] - v2[1]);

    return Object.fromEntries(
      measure === 'cosine' ?
      vectorsWithDistances.reverse().slice(0, results)
      : vectorsWithDistances.slice(0, results)
    );
  }

  distance(vector, otherVector, measure) {
    return this[measure].call(this, vector, otherVector)
  }

  euclidean(vec_a, vec_b) {
    return Math.sqrt(
      this.sumForEach((a_i, b_i) => (a_i - b_i) ** 2, vec_a, vec_b)
    )
  }

  manhattan(vec_a, vec_b) {
    return this.sumForEach((a_i, b_i) => Math.abs(a_i - b_i), vec_a, vec_b)
  }

  dotProduct(vec_a, vec_b) {
    return this.sumForEach((a_i, b_i) => a_i * b_i, vec_a, vec_b)
  }

  cosine(vec_a, vec_b) {
    return this.dotProduct(vec_a, vec_b) / (this.magnitude(vec_a) * this.magnitude(vec_b))
  }

  magnitude(vec) {
    return Math.sqrt(this.sumForEach(v_i => v_i ** 2, vec))
  }

  sumForEach(fn, ...vectors) {
    return vectors[0].reduce((acc, v_i, i) => {
      return acc + fn(...vectors.map(v => v[i]));
    }, 0);
  }
}

Now, rather than manually create vectors, we only use the words, and the transformers library does this for us.

现在，我们不需要手动创建向量，只需使用单词，而转换器库会为我们完成这项工作。

import { pipeline } from '@xenova/transformers';
let extractor = await pipeline('feature-extraction');
let generateEmbedding = (word) => extractor(word, { pooling: "mean", normalize: true })

let vehicles = [
  'car',
  'bicycle',
  'tricycle',
  'motorcycle',
  'sailboat',
  'ship',
]

let vehicleEmbeddings = await Promise.all(vehicles.map(name => generateEmbedding(name)))
let vehiclesMap = Object.fromEntries(vehicles.map((name, i) => [name, vehicleEmbeddings[i]]))

This takes a few seconds to run on my machine the first time (not much, but noticeable), which shows that running ML models, even ones as small as this involve a lot of CPU time.

在我的机器上第一次运行这个模型需要几秒钟（不多，但很明显），这表明运行 ML 模型，即使像这样小的模型，也需要大量的 CPU 时间。

If you’re curious to see what the generated embeddings look like, here’s what the embedding for car is:

如果你想看看生成的嵌入结果是什么样的，下面是 car 的嵌入结果：

Tensor {
  dims: [ 1, 384 ],
  type: 'float32',
  data: Float32Array(384) [
    -0.031706273555755615,     0.1090739443898201,   0.012603563256561756,
      0.05875611677765846,   -0.03913160786032677,   0.032443128526210785,
    ... 378 more items
  ],
  size: 384
}

This thing is huge! I’m not familiar with the details, but it appears that “car” has been turned into a 384-dimension vector.

这东西真大！我对细节不太熟悉，但 “汽车 “似乎已经变成了一个 384 维的矢量。

Let’s see how the search does. We can’t put in a random vector as before, since the embeddings are now controlled by the transformer, but let’s see what happens when we search for a vehicle not in our dataset.

让我们看看搜索效果如何。我们不能像以前那样输入随机向量，因为嵌入现在是由转换器控制的，但让我们看看搜索数据集中没有的车辆时会发生什么。

async function search(word) {
  let p = await generateEmbedding(word)
  console.log("Euclidean:")
  console.log(db.findSimilar(p, 'euclidean'))
  console.log("Manhattan:")
  console.log(db.findSimilar(p, 'manhattan'))
  console.log("Cosine:")
  console.log(db.findSimilar(p, 'cosine'))
}
search('e-bike')

Euclidean:
{
  bicycle: 0.8344609209916007,
  motorcycle: 0.8977509140426253,
  tricycle: 0.9996304153817714
}
Manhattan:
{
  bicycle: 13.002568852846004,
  motorcycle: 13.984138461616215,
  tricycle: 15.961311867872588
}
Cosine:
{
  bicycle: 0.6518374948251899,
  motorcycle: 0.597021662747392,
  tricycle: 0.5003696104110993
}

These are pretty good results. An e-bike is indeed most similar to a bicycle (it is a kind of bicycle), and then a motorbike, and a distant cousin, the tricycle. All three measures return similar rankings.

这些都是相当不错的结果。电动自行车确实与自行车最相似（它是自行车的一种），然后是摩托车，以及远亲三轮车。三者的排名都很接近。

Searching for “truck”: 搜索 “卡车”：

Euclidean:
{
  car: 0.8310878560616409,
  motorcycle: 0.9929289945588754,
  bicycle: 1.005725251152928
}
Manhattan:
{
  car: 12.967854919763596,
  motorcycle: 15.50279750485964,
  bicycle: 15.86006192120071
}
Cosine:
{
  car: 0.6546464440552332,
  motorcycle: 0.5070459014501628,
  bicycle: 0.4942582474585483
}

And searching for “speedboat”:

搜索 “快艇”：

Euclidean:
{
  sailboat: 0.688214933677928,
  ship: 0.9114324817410895,
  car: 1.0909516960778003
}
Manhattan:
{
  sailboat: 10.658648524569825,
  ship: 14.01096388567844,
  car: 16.868695075216202
}
Cosine:
{
  sailboat: 0.7631800985510027,
  ship: 0.5846454070601506,
  car: 0.40491218686683284
}

Nice! 不错！

---

Well, that was pretty cool. We started with looking at vectors and bridging them to dimensions for non-numerical items, and we ended with building our own vector search engine and using a transformer to generate the vectors. This is still a long way from anything you’d use in production, but it’s a good start in understanding what goes on under the hood.

嗯，这很酷。我们从矢量开始，将它们与非数字项目的维度联系起来，最后我们建立了自己的矢量搜索引擎，并使用转换器生成矢量。虽然这离你在生产中使用的任何东西还很远，但这是了解引擎盖下发生了什么的一个良好开端。

Interesting reads 有趣的阅读

The tweet and demo that gave me the idea for this post.

这条推文和演示让我萌生了写这篇文章的想法。

These aren’t specifically about vector search, but explain some of the foundations:

这些内容并非专门针对矢量搜索，但解释了其中的一些基础：

• Khan Academy: Linear Algebra (vectors)

  可汗学院：线性代数（向量）

• MIT OpenCourseWare: Introduction to Machine Learning

  麻省理工学院开放课程：机器学习入门

On vector search: 关于矢量搜索

• Algolia has a good intro to vector search: https://www.algolia.com/blog/ai/what-is-vector-search/

  Algolia 对矢量搜索做了很好的介绍： https://www.algolia.com/blog/ai/what-is-vector-search/

• Meilisearch, on combining full-text search and vector search: Full-text search vs vector search

  Meilisearch，关于全文搜索与矢量搜索的结合：全文搜索与矢量搜索

• Elasticsearch docs on how to tune k-Nearest Neighbour search (a form of vector search) in Elasticsearch

  关于如何调整 Elasticsearch 中 k-Nearest Neighbour 搜索（一种向量搜索）的 Elasticsearch 文档

Applications: 应用：

• Comparing vector search in eCommerce to other search approaches 电子商务中的矢量搜索与其他搜索方法的比较
• How Spotify Uses Semantic Search for Podcasts Spotify 如何将语义搜索用于播客
• Vector embeddings + personalized search 矢量嵌入+个性化搜索

On feature engineering: 关于特征工程

• Two posts explaining feature engineering in Natural Language Processing.

  两篇文章解释了自然语言处理中的特征工程。

On vector databases: 关于矢量数据库

• Comparison of vector databases 向量数据库比较

---

I write about my software engineering learnings and experiments. Stay updated with Tentacle: tntcl.app/blog.shalvah.me.